Jusqu’à quelle distance le regard d’un être humain mesurant 1,80 mètre peut-il porter ? Admettons que celui-ci se hisse sur une échelle, la ligne d’horizon s’en trouve proportionnellement modifiée. Considérant qu’aucun obstacle ne vient obstruer la vue, et que les variations de température en altitude ne contrarient pas la perception, un être humain peut-il voir le mont blanc depuis la tour Eiffel ?
Du haut de ses 4 810 mètres, le mont Blanc est le plus haut sommet de France et d’Europe occidentale. Il est visible depuis plusieurs villes de l’est, de la France, de Suisse et d’Italie. Une légende urbaine prétendait même qu’il était visible depuis le sommet de la tour Eiffel par temps clair.
Le problème de la visibilité d’une structure, d’un monument ou d’une montagne est en première approximation assez simple moyennant certaines conditions et hypothèses. La première est bien sûr de ne pas avoir d’obstacle entre l’observateur et l’objet observé. Une autre hypothèse, et l’on verra qu’elle n’est pas si évidente, est que la lumière se déplace en ligne droite. Enfin, nous admettons que nous sommes à la surface d’une planète sphérique de rayon R=6 371 kilomètres.
Une application du théorème de Pythagore
Sachant que l’on cesse de voir un objet lorsque celui-ci disparaît sous la ligne d’horizon, il est très simple de calculer la distance maximale D à laquelle on peut voir un objet de hauteur h en utilisant le théorème de Pythagore. Rappelons que ce fameux théorème nous dit que dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés.
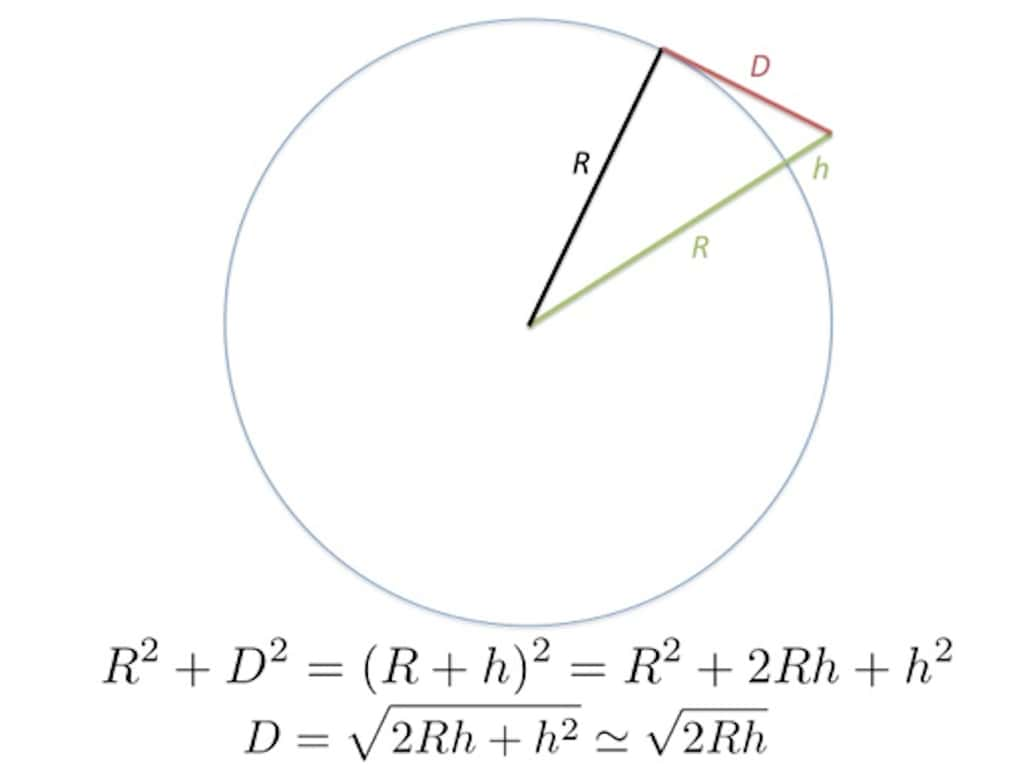
Or, dans le cas d’un objet éloigné vu par un observateur sur l’horizon, on note que le centre de la Terre, la position de l’observateur et celle de l’objet observé forment un triangle rectangle dont l’hypoténuse est R+h tandis que les deux autres côtés ont pour longueurs respectives R et D comme indiqué sur la figure ci-dessous.
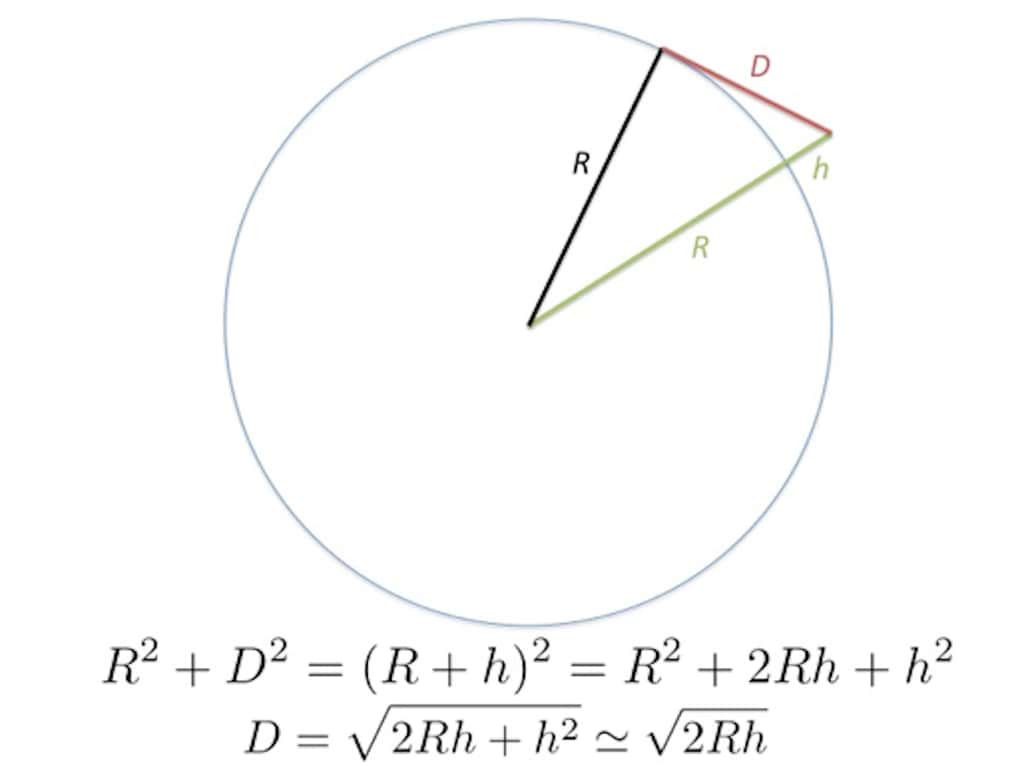
THÉORÈME DE PYTHAGORE DANS UN TRIANGLE RECTANGLE FORMÉ PAR LE CENTRE DE LA TERRE, LA POSITION DE L’OBSERVATEUR ET L’OBJET À OBSERVER.
L’application du théorème de Pythagore permet de calculer la distance maximale de visibilité d’un objet à la surface de la Terre comme étant égale à D=√(2Rh+h2) se réduisant même à √2Rh lorsque la hauteur de l’objet considéré est négligeable devant le rayon de la Terre, ce qui est très souvent le cas.
Calculons maintenant quelques distances de visibilité typiques. Un être humain d’1m80 peut typiquement être vu jusqu’à 4,79 kilomètres. Notons également que c’est la distance maximale à laquelle des yeux situés à 1m80 du sol peuvent voir en l’absence d’obstacle. La cathédrale de Chartres est bien visible de la plaine de la Beauce.
Sa flèche située à 113 mètres de haut et le faitage du toit de sa nef situé à 51 mètres sont visibles respectivement à 37,9 kilomètres et 25,5 kilomètres. La tour Eiffel haute de 324 mètres est visible à 64,2 kilomètres et le mont Blanc à 247,5 kilomètres.
OBJET D’UNE HAUTEUR H2 VUE PAR UN OBSERVATEUR SITUÉ À UNE HAUTEUR H1.
Le fait d’être soi-même en hauteur permet bien entendu d’augmenter la distance à laquelle on peut voir un objet. Si on observe d’une hauteur h1 un objet situé à une hauteur h2, alors la distance d’où on pourra voir l’objet sera égale à la somme de la distance d’où on peut voir l’objet (en h2) au niveau du sol avec la distance d’où on peut voir la hauteur h1 au niveau du sol. On a alors D=D1+D2=√(2Rh1)+√(2Rh2) (Figure ci-dessus).
Quand la lumière ne se propage pas en ligne droite
Si on ajoute la distance à laquelle on peut voir la tour Eiffel à la distance à laquelle on peut voir le mont Blanc, on obtient une distance de 311,7 kilomètres. Si ces deux points étaient éloignés d’une distance inférieure à cette valeur, on pourrait voir le mont Blanc de la tour Eiffel. Une correction supplémentaire doit cependant être prise en compte dans certaines conditions.
En effet, le fait que la température de l’air diminue avec l’altitude fait que les propriétés optiques de l’air varient et que la lumière ne se propage plus exactement en ligne droite.
Dans des conditions où la différence de température est particulièrement marquée et pour des objets de plusieurs kilomètres comme des massifs montagneux, les rayons sont déviés par l’atmosphère d’un angle α d’environ un demi-degré. À la surface d’une planète sphérique, cette déviation se traduit par une distance supplémentaire égale à Rα= 55 kilomètres.
Compte tenu du fait que la distance du mont Blanc à Paris est égale à 475,7 kilomètres, on remarque donc qu’il n’est pas possible de voir cette montagne depuis la tour Eiffel. En revanche, en raison de cette déviation des rayons lumineux par l’atmosphère, on peut en principe voir le mont Blanc jusqu’à 302 kilomètres, c’est-à-dire jusqu’à Clermont (295 kilomètres), Marseille (302 kilomètres), Nîmes (295 kilomètres) mais pas Strasbourg (314 kilomètres).
Pour avoir précisément les zones de visibilité du mont Blanc, il faut tenir compte des obstacles sur la ligne de visée. En utilisant un modèle numérique de terrain, il est possible avec certains logiciels de calculer les zones d’ombre en plaçant dans ce modèle une source de lumière au sommet de Mont-Blanc.
La géographe Claire Medici a effectué ce calcul qui peut être visualisé ici. Le résultat est saisissant et montre que le mont Blanc est visible de nombreuses régions allant du plateau de Langres aux Cévennes, au Puy-de-Dôme et à la plaine du Pô en passant par les Monts du Lyonnais et les massifs des Vosges et du Jura.
futur






